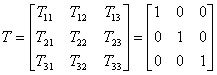|
גיאומטריה של מרחב עקום
דמיינו חיידק שחי בתוך הקרום הדק של בועת סבון. אנחנו יכולים לראות שצורתה של בועת הסבון היא כדורית כי היא מוכלת בחלל התלת-מימדי השטוח שלנו, אליו ניתן לייחס אותה. מנקודת מבטו של החיידק הוא חי בעולם דו מימדי. בכל נקודה שבה הוא נמצא הוא יכול לנוע לשני כיוונים ניצבים. בשבילו הכיוון לתוך הבועה או החוצה ממנה אינו קיים. אבל החיידק יכול בכל זאת להבין שהעולם הדו-מימדי שלו איננו שטוח. שני קווים "ישרים" (גיאודזיים) יתקרבו זה אל זה במרחק וגם סכום הזויות במשולש יהיה גדול מ-°180. זאת משום שלבועת הסבון יש עקמומיות פנימית. אילו לעולמו של החיידק הייתה צורת גליל הוא לא היה יכול לדעת שהעולם שלו עקום. לבד מהעובדה שבמרבית הכיוונים אם ילך מרחק רב מאד הוא יגיע באופן מפתיע לנקודה מוכרת, הוא לא יבחין בגיאומטריה של עולמו בשום דבר שונה מזו של מרחב דו-מימדי שטוח (מישור). לגליל יש עקמומיות חיצונית בלבד. כאשר אנחנו מנסים לחקור את החלל התלת-מימדי או את החלל-זמן ה-4 מימדי שלנו אנחנו במצב דומה לאותו חיידק. אנחנו יכולים להסתכל עליהם ולמדוד אותם רק מבפנים. אין אנו יכולים להניח שיש מרחב בעל מספר גדול יותר של מימדים שמכיל אותם. כמובן שאנחנו יכולים לדבר רק על העקמומיות הפנימית שלהם.
ווקטורים משיקים ומרחבים משיקים
אנו יודעים שווקטור הוא דבר שיש לו גודל וכיוון. אבל כשמדברים על מרחב עקום המושג כיוון הוא קצת חמקמק. אם החיידק שלנו בבועה יצביע קדימה, אנחנו, היצורים התלת-מימדיים, נוכל לראות שהוא למעשה מצביע לכיוון שיוצא אל מחוץ לעולם שלו. כאשר הוא מצביע לכיוון כלשהו הוא מתווה קו שמשיק למשטח העקום בנקודה שבה הוא עומד. אם הוא יתקדם מרחק מה ישר קדימה ואז יצביע שוב קדימה נוכל אנחנו לראות שהוא מצביע לכיוון אחר. כמובן שהחיידק לא יכול לראות זאת, אבל מכיוון שהוא יודע שהעולם שלו עקום הוא יכול להניח שכזאת היא התמונה. לכל נקודה במשטח עקום ישנו משטח ישר (מישור) שמשיק למשטח העקום. אפשר להתוות את כל הכיוונים האפשריים של המשטח העקום בנקודה זו בתוך המישור המשיק. באותו אופן לכל נקודה במרחב תלת-מימדי עקום או בחלל-זמן 4-מימדי עקום אפשר להגדיר מרחב שטוח משיק שבו ניתן להתוות את כל הכיוונים של המרחב העקום. לכן בגיאומטריה דיפרנציאלית מדברים לרוב על ווקטורים משיקים ולא על ווקטורים סתם. איך מחשבים את אורכו של קו עקום? אנחנו יודעים לחשב את אורכו של קו ישר, ולכן אפשר לחשב בקירוב את אורכו של קו עקום על ידי חלוקתו להרבה קטעים שהם מספיק קטנים בכדי להחשיבם לישרים וסיכום אורכם של כל הקטעים האלה. בחשבון דיפרנציאלי, שאני מנסה להימנע מלהשתמש בו במאמר זה, אפשר להקטין את גודל הקטעים לאפס ולהגדיל את מספרם לאין-סוף ולחשב את אורכו המדויק של קו עקום. בגיאומטריה דיפרנציאלית שעוסקת במרחבים עקומים עושים דבר דומה. אנחנו יודעים את כללי הגיאומטריה של מרחב שטוח. לוקחים פיסה מהמרחב העקום מסביב לנקודה, פיסה קטנה מספיק כדי להיחשב שטוחה, ועושים את החישובים הגיאומטריים עבור הפיסה הזאת תוך שימוש במרחב המשיק לאותה נקודה. אם רוצים לחשב גדלים עבור חלק גדול יותר של המרחב, אנחנו מחלקים אותו להרבה פיסות קטנות כאלה ומסכמים עבור כל המרחב הדרוש (או משתמשים בחשבון דיפרנציאלי ומחשבים את האינטגרל על כולו).
הכלי המתמטי העיקרי בתורת היחסות הכללית הוא חשבון טנסורי. נזכיר כאן רק מעט מתוך תחום מתמטי נרחב זה. נגדיר שני סוגים של טנסורים שנזדקק להם כאן:
טנסור מסדר (0,n) הוא פונקציה לינארית שמקבלת n ווקטורים ומחזירה מספר.
טנסור מסדר (1,n) הוא פונקציה לינארית שמקבלת n ווקטורים ומחזירה ווקטור.
ההגדרות האלה שונות במקצת מההגדרה הכללית של טנסור מסדר (n,m) אבל הן שקולות לה ופשוטות יותר.
ווקטורים לא מוגדרים בהכרח על ידי קואורדינאטות, אבל זוהי דרך נוחה להגדיר אותם אם רוצים לעשות עליהם חישובים. בוא נראה דוגמה: המכפלה הסקלארית של ווקטורים מתקבלת על ידי טנסור מסדר (0,2). הטנסור מקבל שני ווקטורים ומחזיר מספר. המשוואה הטנסורית הכללית של הפעולה יכולה להיכתב כך:
אם נבחר מערכת קואורדינאטות ונייצג את U ואת V על-ידי הקואורדינאטות שלהם באופן הבא:
או כפי שנהוג לכתוב בחשבון טנסורי:
(מציין עליון בחשבון טנסורי הוא אינדקס של איבר של ווקטור. כדי לציין פעולת חזקה שמים את האיבר בתוך סוגריים)
כאשר משתמשים בקואורדינאטות מייצגים את הטנסור T של המכפלה הסקלרית על ידי מטריצה בת n x n איברים כאשר n הוא מספר המימדים במרחב שלנו. האיברים של המטריצה משמשים כמקדמים של הביטויים במשוואת הפונקציה. אנחנו יודעים שהמכפלה הסקלרית של ווקטורים תלת-מימדיים נתונה על-ידי:
הערך x איננו תלוי במערכת הקואורדינאטות וגודלו יהיה זהה בכל מערכת קואורדינאטות שנבחר (הערך שלו תלוי כמובן ביחידות שנבחר). אפשר לכתוב את המכפלה הסקלרית כמשוואה ווקטורית באופן הבא:
הפירוש של הכתוב הוא: קחו את כל הצירופים האפשריים של i ו-j וסכמו את האיברים שבנויים מהמכפלה של האיבר ה-ij של המטריצה T הרכיב ה-i של הווקטור U והרכיב ה-j של הווקטור V. מכיוון שאנו עובדים בשלושה מימדים, i ו-j יכולים לקבל ערכים מ-1 עד 3. כדי לחסוך קצת כתיבה איישטיין קבע מוסכמה שנקראת "מוסכמת הסיכום של איינשטיין" והיא אומרת כך: בכל פעם שאינדקס מופיע בדיוק פעמיים באיבר מסכמים אותו עבור כל הערכים האפשריים של אותו אינדקס. אם משתמשים במוסכמה זו ניתן לכתוב את (2) פשוט כך:
(2.1) נותנת לנו סכום של 9 איברים בעוד שב- (1) ישנם רק שלושה איברים. אלה הם האיברים שבהם i=j. כמו כן המקדמים של האיברים ב-(1) כולם שווים ל-1. המטריצה T תראה לכן כך:
מה ההבדל בין אינדקסים עליונים לאינדקסים תחתונים? הם משמשים לסוגים שונים של ישויות מתמטיות. כפי שראינו אינדקסים עליונים משמשים עבור ווקטורים. אינדקסים תחתונים לעומתם משמשים עבור גראדיינטים. גראדיינט מציין את השינוי של תכונה מסוימת לכל יחידת מרחק. למשל, בנקודה כלשהי על פני כדור הארץ, בכמה משתנה לחץ האוויר לכל מטר בכל אחד מהכיוונים. איברים של טנסור יכולים לקבל גם אינדקסים עליונים וגם אינדקסים תחתונים. יש להם אינדקס תחתון אחד לכל ווקטור שהם מקבלים ושאר האינדקסים – אם יש כאלה – הם עליונים. ווקטורים וגראדיינטים מתנהגים בצורה שונה במעבר בין מערכות קואורדינאטות. למשל, אם מקטינים את יחידות המידה איברי הווקטור יהיו גדולים יותר ואיברי הגראדיינט, שבהם יחידות הקואורדינאטות נמצאות במכנה, יקטנו. דברים שמתנהגים כמו ווקטורים נקראים קונטרה-ווריאנטים ודברים שמתנהגים כמו גרדיינטים נקראים קו-ווריאנטים. בחלל-זמן שבו 4 מימדים משתמשים באינדקסים 0 עד 3 עבור קואורדינאטות, כאשר רכיב הזמן מצוין באינדקס 0.
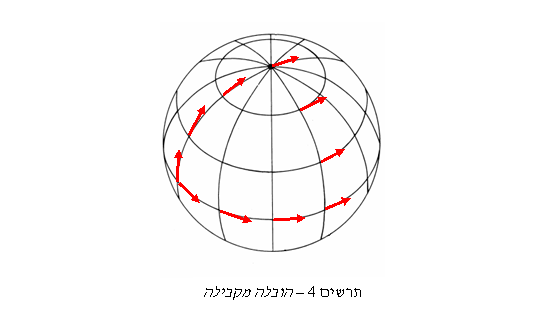
הובלה מקבילה היא פעולה שבה מובילים ווקטור לאורך מסלול מבלי לשנות את אורכו או לסובב אותו (יחסית למרחב). במרחב שטוח אפשר לומר שהווקטור המובל מקביל לווקטור המקורי בכל נקודה לאורך המסלול. במרחב עקום אי אפשר לומר זאת. בואו נסתכל על פני השטח של כדור הארץ כדי להראות זאת: נתחיל בקו המשווה בנקודה שבה קו האורך 0 חוצה אותו כשאנו מחזיקים חץ שמצביע צפונה (תרשים 4). ננוע לאורך קו האורך 0 עד לקוטב הצפוני כשאנחנו שומרים שהחץ שלנו יהיה מקביל לאדמה ויצביע קדימה כל הזמן. כשנגיע לקוטב הצפוני החץ שלנו יראה לכיוון קו האורך 180°. כעת נתחיל לנוע דרומה לאורך קו האורך 90° מזרח כשהחץ שלנו ניצב למסלול התנועה כפי שהיה בקוטב הצפוני. כשנגיע לקו המשווה יצביע החץ שלנו מזרחה. נמשיך מערבה לאורך קו המשווה עד לנקודת ההתחלה כשהחץ מצביע כל הזמן לאחור. למרות שלא סובבנו את החץ לכל אורך הדרך חזרנו לנקודת ההתחלה כשהחץ מסובב ב-90° יחסית למצבו המקורי. ברור שלא נוכל לטעון שהוא עכשיו מקביל למצבו המקורי. משמעות הדבר היא שהמוסג "כיוון" לא יכול להיות מוגדר באופן גלובלי במרחב עקום. אנחנו יכולים להשוות כיוונים של שני ווקטורים רק אם הם נמצאים באותה הנקודה. העובדה שהובלה מקבילה לאורך לולאה סגורה משנה את כיוונו של ווקטור במרחב עקום אך לא במרחב שטוח יכולה להוביל לרעיון להשתמש בה כדרך למדוד עקמומיות. לא נוכל להוכיח זאת כאן מתמטית, אבל מסתבר שאם בוחרים לולאה מספיק קטנה מסביב לנקודה במרחב עקום, מידת הסטייה של ווקטור שמובל מקבילית לאורכו היא יחסית לשטח הכלוא על ידי הלולאה. כך שהיחס בין שטח הלולאה ומידת שינוי הכיוון של הווקטור (באיזו דרך שנבחר למדוד אותה) יכולה לשמש מדד לעקמומיות המשטח שמכיל את הלולאה. למעשה אנחנו מגדירים את העקמומיות באמצעות היחס הזה.
טנסור רימן הנו טנסור מסדר (1,3) שמתאר את העקמומיות בכל הכיוונים בנקודה מסוימת במרחב. הוא מקבל שלושה ווקטורים ומחזיר ווקטור אחד. הווקטורים שמוזנים לטנסור צריכים להיות קטנים מאוד והאורך שלהם הוא ε. אם משתמשים בשני הווקטורים הראשונים ליצירת מקבילית זעירה ומובילים מקבילית את הווקטור השלישי מסביב למקבילית הזאת, הווקטור שמחזיר הטנסור הוא בקירוב ההפרש הווקטורי בין הווקטור המקורי לווקטור שלאחר ההובלה המקבילה. אפשר לכתוב זאת בצורה מתמטית כך:
כאשר U ו-V הם הווקטורים באורך ε שיוצרים את המקבילית, R הוא טנסור רימן, W הוא הווקטור השלישי במצבו המקורי ו– W'הוא הווקטור אחרי ההובלה המקבילה. שימו לב ש- ε3 קטן מהר יותר מ- ε2כאשר מקטינים את ε, ולכן לכל דיוק רצוי נוכל לבחור ε קטן מספיק כדי שהביטויים המכילים ε3 יהיו זניחים ונוכל לכתוב:
אם משתמשים בקואורדינאטות זה נראה כך:
R הוא כעת מטריצה 4-מימדית בעלת (N)4 איברים כאשר N הוא מספר המימדים במרחב. על ידי סיכום עבור j,k ו-l נוכל למצוא כל איבר של הווקטור שמהווה את ההפרש בן W ל-W'. אפשר לראות את הווקטור הזה כווקטור שמחבר את הקצוות של W ו-W'.
המטריקה היא מושג חשוב מאד בגיאומטריה של מרחב עקום. היא מאפשרת לנו לחשב גדלים של ווקטורים וזוויות בין ווקטורים. אלה הם בעצם הדברים שאנחנו רוצים לדעת לגבי ווקטורים. המטריקה הינה טנסור מסדר (0,2). היא מקבלת שני ווקטורים ומחזירה מספר. במרחב אאוקלידי המטריקה מוגדרת כמכפלה הסקאלארית של שני ווקטורים, זו שהראינו בסעיף הדן בטנסורים למעלה. אם נזין את הטנסור הזה באותו ווקטור פעמיים, המספר שנקבל יהיה ריבוע האורך של הווקטור. אם נזין אותו בשני ווקטורים שונים, המספר שיתקבל יהיה המכפלה של אורכי הווקטורים כפול קוסינוס הזווית שביניהם. אחרי שאנחנו יודעים את אורכי הווקטורים אנחנו יכולים להשתמש במטריקה לחישוב הזווית שביניהם. בחלל-זמן שטוח (שקרא מרחב מינקובסקי) המטריקה או המכפלה הפנימית של שני ווקטורים מוגדרת בצורה דומה, רק שרכיב הזמן מופיע בה בסימן הפוך. הראנו ב"להבין את תורת היחסות הפרטית" שהמטריקה של חלל-זמן דו מימדי נתונה על-ידי:
במרחב-זמן 4-מימדי היא תהיה:
או אם נכתוב אותה כטנסור:
מסכמים עבור i ו-j שמקבלים ערכים מ-0 עד 3. המטריצה g תראה כך:
למטריצה של המטריקה יש צורה אלכסונית יפה כזאת רק בגלל האופן שבו בחרנו את מערכת הקואורדינאטות, או ליתר דיוק, בגלל שהקואורדינאטות אינן תלויות אחת בשנייה (אורתוגונליות). אם נבחר את הקואורדינאטות באופן אחר, האיברים באלכסון לא יהיו שווים ל-1 ויתר האיברים במטריצה לא יהיו שווים ל-0. במרחב או בחלל-זמן שטוחים אפשר לבחור מערכת קואורדינאטות אורתוגונלית ולהשתמש בה עבור כל המרחב. במרחב עקום אין מערכת קואורדינאטות גלובלית. אפשר אמנם לבחור מערכת כזאת במרחב המשיק של כל נקודה ונקודה, אבל פירוש הדבר יהיה שאנו משנים את מערכת הקואורדינאטות במעבר מנקודה לנקודה. אם נרצה לערוך חישובים לגבי תחום במרחב או בחלל-זמן, נזדקק לתיאור מתמטי של השתנות מערכת הקואורדינאטות במעבר מנקודה לנקודה. במתמטיקה משתמשים במושג הנגזרת כדי לתאר איך משהו משתנה במרחב. הדבר פשוט יחסית כאשר יש לנו מערכת קואורדינאטות גלובלית כמו למשל במקרה של משטח כדורי המוכל בתוך מרחב אאוקלידי תלת-מימדי. זה נעשה קשה יותר כאשר יש לעשות זאת ללא מערכת יחוס גלובלית (זוכרים את החיידק בבועה?). המתמטיקה מגדירה לצורך כך מושג חדש וקוראת לו נגזרת קו-ווריאנטית. בעזרת הכלי הזה מתמטיקאים יכולים לכתוב משוואה שקושרת את איברי טנסור המטריקה עם האיברים של טנסור העקמומיות של רימן. המשוואה הזאת מפחידה למדי ומלאה בסימנים מבהילים ואפילו לא נתחיל לדון בה כאן. לאלה שהנם אמיצים מספיק כדי להציץ ולראות איך היא נראית, מילות המפתח שלכם הן "Christoffel symbols" וגם "metric connection".
טנסור ריצ'י, טנסור ווייל וסקלר ריצ'י
לטנסור רימן יש 256 איברים בחלל-זמן 4-מימדי. למרבה המזל ישנן כמה קבוצות של איברים זהים או שונים רק בסימנם. ישנן גם קבוצות איברים שסכומן שווה ל-0. אם לוקחים את כל אלה בחשבון, יוצא שישנם בטנסור רימן רק 20 איברים בלתי תלויים שמהם ניתן למצוא את כל האיברים בטנסור. טנסור ריצ'י הוא טנסור מסדר (0,2) שניתן למוצאו מתוך טנסור רימן ע"י הנוסחה הבאה:
כדי לעשות את הדברים עוד יותר לא ברורים מאשר הנם ממילא, המתמטיקאים מסמנים באות R גם את טנסור רימן, גם את טנסור ריצ'י וגם את סקלר ריצ'י. אפשר להבחין ביניהם רק לפי מספר האינדקסים שלהם: 4 אינדקסים לטנסור רימן, 2 לטנסור ריצ'י וללא אינדקס לסקלר ריצ'י. המשוואה שלמעלה אומרת שכל רכיב Rik של טנסור ריצ'י מחושב על-ידי סיכום כל הרכיבים של טנסור רימן שבהם האינדקס השני הוא i האינדקס הרביעי הוא j והאינדקס הראשון והשלישי זהים. טנסור ריצ'י תלוי רק ב-10 מתוך 20 האיברים הבלתי תלויים של טנסור רימן. טנסור ריצ'י עצמו הוא סימטרי לאלכסון ולכן בחלל-זמן 4-מימדי יש לו 10 רכיבים בלתי תלויים מתוך 16 האיברים שלו. אפשר לומר שטנסור ריצ'י מייצג 10 מתוך 20 האיברים הבלתי תלויים של טנסור רימן. יתר 10 האיברים הבלתי תלויים של טנסור רימן מיוצגים על-ידי טנסור ווייל (Weyl). לטנסור ווייל יש מבנה דומה לזה של טנסור רימן, אבל בנוסף לכל התלויות האחרות בין האיברים שבטנסור רימן, גם כל האיברים של טנסור ריצ'י שווים בו ל-0. כלומר:
לטנסור ווייל ישנם גם כן 256 איברים אבל רק 10 מהם הנם בלתי תלויים. סקלר ריצ'י הוא מספר שמחושב על-ידי הנוסחה:
כאשר gij נקרא הטנסור ההופכי של המטריקה וניתן לחשבו מתוך המטריקה gij.
המשמעות הגיאומטרית של טנסורי העקמומיות
לנקודה (0 מימדים) לא יכולה להיות עקמומיות. לקו (מימד אחד) יכולה להיות רק עקמומיות חיצונית. אי אפשר להוביל עליו ווקטור לאורך לולאה. אפשר לאפיין את העקמומיות החיצונית של קו בנקודה מסוימת על-ידי הרדיוס המקומי. שניים הוא מספר המימדים הקטן ביותר שבו יכולה להיות עקמומיות פנימית. הדוגמה של משטח כדורי היא מקרה פשוט מאד של שני מימדים. יש בו רדיוס זהה בכל נקודה ובכל כיוון. בדוגמה כללית יותר של משטח עקום יכול להיות בנקודה רדיוס שונה בכיוונים שונים, כמו למשל במקרה של אליפסואיד. אבל רדיוס הוא תכונה שאפשר לדבר עליה רק מנקודת מבט חיצונית. מבפנים אנחנו יכולים רק לדבר על התוצאה של הובלה מקבילה לאורך מקבילית זעירה. בשני מימדים הווקטור המקורי והווקטור שאחרי ההובלה מוכלים שניהם במישור המשיק לנקודה. מכיוון שאורך הווקטור אינו משתנה בהובלה מקבילה, ההבדל בין הווקטורים יכול להתבטא רק בזווית שביניהם. מסתבר שהזווית הזאת איננה תלויה במקבילית שנבחר אלא רק בשטחה. לכן כל המידע על העקמומיות הפנימית של משטח עקום בנקודה מסוימת נתון על-ידי מספר אחד. בגיאומטריה דיפרנציאלית סקלר ריצ'י נותן לנו את כל המידע על העקמומיות של משטח דו-מימדי עקום. ניתן למצוא את כל 4 האיברים של טנסור ריצ'י דו-מימדי ואת 16 האיברים של טנסור ווייל דו-מימדי מתוך הסקלר היחיד הזה. דרך נוספת לבחון את העקמומיות הפנימית היא באמצעות הסטייה הגיאודזית. אנו יודעים שבמשטח עקום קווים גיאודזיים שהנם מקבילים באזור מסוים נעשים מוטים ומשנים את המרחק ביניהם כאשר מתקדמים לאורכם. הם מתקרבים במשטח כדורי או באליפסואיד ומתרחקים בהיפרבולואיד (משטח דמוי אוכף). כל נקודה במשטח עקום יכולה להיות אליפסואידית, שטוחה או היפרבולואידית מקומית. אם ניקח קו קצר מאוד בנקודה מסוימת על המשטח ונתחיל להזיז את כל הנקודות שלו לאורך קווים גיאודזיים ניצבים אליו, הקו ישנה את אורכו. בנקודת ההתחלה הקווים הגיאודזיים מקבילים ולכן אורך הקו אינו משתנה; אבל כבר אז מתחיל להשתנות קצב השינוי של האורך (לו השתמשתי בחשבון דיפרנציאלי – ואינני עושה זאת – הייתי אומר שהנגזרת השנייה של האורך שונה מאפס). אפשר לחשוב על האנלוגיה הבאה: כאשר אנחנו מפילים משהו, ברגע שמרפים ממנו מהירותו עדיין שווה לאפס אבל תאוצתו כבר שווה לתאוצת הכבידה. הקצב הזה שבו הקו הזעיר מתחיל לשנות את אורכו הוא הסטייה הגיאודזית בנקודה. במשטח עקום דו מימדי היא תהיה תמיד שווה בכל הכיוונים. בשלושה מימדים נזדקק ל-6 מספרים כדי לתאר באופן מלא את העקמומיות בנקודה. ברור שסקלר ריצ'י לא יספיק לנו כאן. טנסור ריצ'י בשלושה מימדים הוא בעל 9 איברים, אבל משום שהוא סימטרי לאלכסון רק 6 מהם הם בלתי תלויים. טנסור ריצ'י יכול לספר הכל על העקמומיות של מרחב תלת-מימדי וכל 81 האיברים של טנסור רימן ניתנים לחישוב מתוך טנסור ריצ'י. מה לגבי הסטייה הגיאודזית? ניתן לעשות משהו דומה לזה שעשינו בשני מימדים: ניקח עיגול זעיר ונבחן איך הוא מתחיל להשתנות כאשר מזיזים את כל הנקודות שלו לאורך קווים גיאודזיים הניצבים למישור המעגל. שימו לב שאם קצב השינוי הוא אחיד בכל הכיוונים המעגל ישמור על צורתו ורק ישנה את גודלו, אבל אם קצב השינוי אינו שווה בכל הכיוונים המעגל ישנה את צורתו ויהפוך לאליפסה. ששת האיברים הבלתי תלויים של טנסור ריצ'י יכולים לתאר את השינויים האלה בכל נקודה במרחב תלת-מימדי עקום. ראינו שבמרחב 4-מימדי טנסור רימן הוא בעל 256 איברים שמתוכם 20 הם בלתי תלויים. לפיכך דרושים לנו 20 מספרים כדי לתאר באופן מלא את העקמומיות של מרחב 4-מימדי בנקודה נתונה. כדי לבחון את הסטייה הגיאודזית ניקח כדור זעיר ונסיע את כל הנקודות שלו בכוון המימד הרביעי. גם כאן הכדור יכול לשנות את נפחו וגם לשנות את צורתו לאליפסואיד. 10 האיברים הבלתי תלויים של טנסור ריצ'י מתארים איך הכדור מתחיל לשנות את נפחו בכל כוון אפשרי. טנסור ווייל מתאר איך הכדור מתחיל לשנות את צורתו. אם טנסור ווייל כולו אפסים אבל טנסור ריצ'י לא, הכדור ישנה רק את נפחו ולא את צורתו. אם טנסור ריצ'י כולו אפסים אבל טנסור ווייל לא, הכדור יהפוך לאליפסואיד אבל ישמור על נפחו. ב-4 מימדים ומעלה אפשר לדבר על שני סוגים של עקמומיות: עקמומיות ריצ'י ועקמומיות ווייל. העקמומיות הכוללת של המרחב הנה צירוף של שני סוגי העקמומיות האלה. מה אפשר ללמוד מכל זה? אפשר לראות שהדוגמאות של משטח דו-מימדי עקום שבהן השתמשנו הנן מאוד מוגבלות. למשטח דו מימדי יכולה להיות רק עקמומיות סקלרית ולא עקמומיות ריצ'י או ווייל. החגיגה האמיתית בגיאומטריה של מרחבים עקומים מתחילה ב-4 מימדים שבהם יש גם עקמומיות ריצ'י וגם עקמומיות ווייל. לרוע המזל המוח שלנו מסוגל לדמיין רק 3 מימדים. מכיוון שאנחנו זקוקים למימד אחד שבו נוכל לעקם את החלל שלנו, משטח דו-מימדי עקום הוא המקסימום שאנחנו מסוגלים לדמיין. לכן איננו יכולים לתפוס באמת את המשמעות של עקמומיות ריצ'י או ווייל כפי שאיננו יכולים לראות איך בחלל 4-מימדי שטוח מישור יכול לשמש כציר סיבוב (הוא יכול). אנחנו יכולים לקבל את זה, אנחנו יכולים לחשב את זה, אבל איננו יכולים לדמיין את זה. זו הסיבה שלרוב משתמשים במתמטיקה טהורה כדי לתאר חלל-זמן עקום וכמעט מוותרים לגמרי על הניסיון להבין את משמעות העקמומיות.
|