|
עקרונות תורת היחסות הכללית
פעם, כאשר איינשטיין התכונן להרצאה על תורת היחסות (שאז עוד לא נקראה פרטית), עברה במוחו המחשבה שאדם הנופל מגג של בניין אינו חש כלל במשקלו. מחשבה זו שאותה תאר מאוחר יותר כ"מחשבה המשמחת ביותר בחיי", הייתה הזרע שממנו צמחה תורת היחסות הכללית. הרעיון של תורת היחסות הכללית אינו כה קשה להבנה. המתמטיקה שלה מסובכת למדי וכוללת גיאומטריה של מרחב עקום שכשלעצמה אינה קלה לתפיסה. איינשטיין נאבק במתמטיקה של תורתו במשך כמה שנים לפני שהגיע לגרסה הסופית של משוואת השדה שלו. למרות שהמשוואה נראית פשוטה למדי היא כוללת למעשה 10 משוואות דיפרנציאליות חלקיות שונות ואינה ניתנת לשימוש מעשי כמות שהיא. איינשטיין לא ציפה שפתרון מדויק למשוואה שלו יימצא במהרה. למרבה ההפתעה הפתרון הראשון למשוואה נמצא על ידי קרל שוורצשילד חודשים ספורים בלבד לאחר פרסום הגרסה הסופית של תורת היחסות הכללית ב-1915. הפתרון מתאר את שדה הכבידה סביב גוף מסיבי כדורי במנוחה. פתרונות נוספים למשוואה לא נמצאו עד לשנות השישים, כאשר פותחו כלים מתמטיים חדשים ומחשבים נכנסו לתמונה.
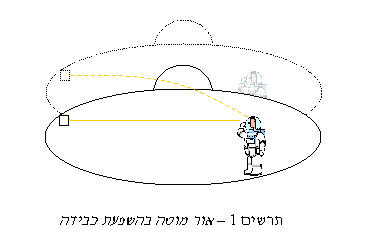
בתוך חללית שנופלת נפילה חופשית הכל נראה חסר משקל. אדם שנמצא בתוך חללית סגורה לא יוכל לדעת אם החללית נופלת נפילה חופשית או שהיא משייטת במהירות קבועה בחלל החיצון, במקום שבו אין כבידה משמעותית. כל ניסוי מכני שיוכל לערוך יראה את אותן התוצאות בשני המקרים. כמו כן, אדם בחללית סגורה לא יוכל לדעת אם החללית שלו חונה על פניו של כוכב לכת או שהיא מאיצה בתאוצה קבועה בחלל הבין כוכבי. איינשטיין גרס שאין כאן רק דמיון של התנהגויות, אלא מצבים פיזיקליים זהים. כלומר, מערכת יחוס בנפילה חופשית בשדה כבידה אקוויוולנטית למערכת אינרטית בהעדר כבידה ומערכת נייחת בשדה כבידה אקוויוולנטית למערכת מאיצה בהעדר כבידה. רגע אחד! ומה לגבי האור? אם האקוויוולנטיות הזו נכונה, הרי שפולס של אור ינוע בקו ישר ביחס למערכת הייחוס הנופלת נפילה חופשית. ביחס לצופה נייח קרן האור תראה מעוקמת כלפי מטה (תרשים 1). האם ייתכן שגם אור מושפע מכבידה? תורת היחסות הכללית מניחה שכך אכן קורה וההנחה הזאת אושרה בתצפיות על אור כוכבים ובניסויים.
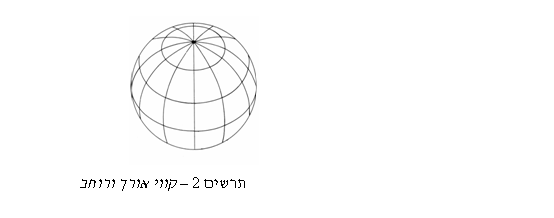
איינשטיין טען שאפשר לראות את הכבידה כעקמומיות בחלל-זמן ולא ככוח שפועל בין גופים. (למעשה מה שאיינשטיין טען היה שהכבידה הנה עקמומיות בחלל-זמן ולא כוח, אבל השאלה מהי כבידה באמת היא שאלה פילוסופית ולא פיזיקאלית ולא נכנס כאן לדיון בה.) איך ניתן להסביר את ההתנהגות של עצמים בשדה כבידה באמצעות עקמומיות בחלל-זמן? כדי להבין זאת נסתכל על מערכת עקומה שכולנו מכירים – פני כדור הארץ. תחילה עלינו למצוא אקוויוולנט לקו ישר במערכת העקומה שלנו. אנחנו יכולים להגדיר קו כזה כנתיב הקצר ביותר בין שתי נקודות, או לחילופין כקו שהנע לאורכו אינו פונה לשום צד ביחס למשטח העקום (הוא פונה רק עם העקמומיות של המשטח). קו כזה נקרא קו גיאודזי. על משטח כדורי יהיה זה מעגל שמרכזו במרכז הכדור. קווי אורך למשל הם קווים גיאודזיים.
כעת תארו לעצמכם שתי ספינות שמתחילות את דרכן בשתי נקודות על קו המשווה ונעות במהירות שווה ישר צפונה. בתחילה נעות שתי הספינות במקביל אחת לשנייה, אבל עם הזמן הן מתחילות להתקרב אחת אל השנייה בכוון מזרח-מערב. אם החלל-זמן עקום בצורה כזאת ששני קווים גיאודזיים בכוון הזמן מתקרבים אחד אל השני בחלל, הרי ששני גופים שמתחילים במנוחה אחד ביחס לשני (נעים רק בכוון הזמן), יתחילו להתקרב אחד אל השני כאילו איזה כוח מושך אותם. ומה אם נרצה לשמור על מרחק קבוע בין שני גופים בשדה כבידה? בואו נסתכל שוב על המודל של פני כדור הארץ. המרחק בין שני קווי רוחב הוא קבוע. אבל קווי רוחב, למעט קו המשווה, אינם קווים גיאודזיים. התקדמות לאורך קו רוחב כרוכה בפניה רצופה ביחס לפני כדור הארץ. אם קשה לך לראות זאת נסה לחשוב על קו רוחב קרוב מאוד לקוטב, למשל מעגל ברדיוס של 10 מטרים מסביב לקוטב. ברור שכדי לנוע לאורכו יש לפנות באופן רצוף. לפיכך, אם רוצים ששתי ספינות שטות ישמרו על מרחק קבוע ביניהן לפחות אחת מהן צריכה לפנות כל הזמן הלאה מהשנייה. בדומה לכך, בשדה כבידה דרוש כוח שיפעל על גוף באופן רצוף כדי לשמור אותו במרחק קבוע מגוף אחר. אפשר לשנות עכשיו במקצת את החוק הראשון של ניוטון ובמקום לומר שללא כוח שפועל עליהם גופים נעים במהירות קבועה לאורך קווים ישרים, נאמר שללא כוח שפועל עליהם גופים נעים לאורך קווים גיאודזיים בחלל-זמן. בהיעדר כבידה החלל-זמן הוא ישר או שטוח (שטוח בהקשר זה משמעותו לא עקום) והקווים הגיאודזיים האלה פירושם יהיה תנועה לאורך קווים ישרים בחלל במהירות קבועה. בסמוך לגופים כבדים החלל-זמן עקום וקוים גיאודזיים בו יתוו תנועה בתאוצה קבועה לאורך קווים ישרים בחלל (נפילה חופשית), תנועה במסלול מסביב לגוף מסיבי או כל התנהגות ידועה אחרת של גופים בשדה כבידה. שדה הכבידה אינו שדה של כוח אלא עקמומיות בחלל-זמן שנוצרת מנוכחות של מסה ואנרגיה.
היסט לאדום והתרחבות זמן כבידתיים
בואו נתאר את התרחיש הבא: חללית גדולה מאוד מאיצה בחלל הבין כוכבי בכיוון שנקרא לו "למעלה". על רצפת החללית ממוקם מקור אור. בזמן שהאור נע מהרצפה אל התקרה מהירות החללית גדלה, כך שכאשר הוא מגיע לתקרה החללית מתרחקת ממקור האור כפי שהיה כאשר האור נפלט ממנו. בשל אפקט דופלר, צופה שנמצא סמוך לתקרה יראה את תדירות האור מוסטת לאדום (נמוכה יותר). באופן דומה צופה על רצפת החללית יראה אור הבא ממקור שעל תקרת החללית מוסט לכחול (תדירות גבוהה יותר). עקרון האקוויוולנטיות מחייב שאותו הדבר יקרה כאשר החללית נמצאת במנוחה על פניו של כוכב לכת. מכאן שאדם שנמצא בראשו של מגדל גבוה יראה אור המגיע מהקרקע מוסט לאדום ואדם על הקרקע יראה אור שבא מראש המגדל מוסט לכחול. תופעה זו נקראת היסט כבידתי לאדום. עכשיו נניח שיש שני מקורות לייזר זהים, אחד על הקרקע והשני בראש מגדל גבוה. אדם שנמצא על ראש המגדל מצויד במכשיר שיכול לספור את המחזורים של גלי האור. הוא מפעיל את המכשיר למשך שנייה אחת בדיוק ומשווה את מספר המחזורים מהאור שבא מהמקור שלידו למספק המחזורים של האור שבא מהקרקע. מכיוון שהאור שבא מהקרקע מוסט לאדום, הוא יספור יותר מחזורים של האור מהמקור העליון מזה של התחתון. אבל האיש יודע ששני המקורות זהים ולכן צופה על הקרקע יספור את אותו מספר מחזורים לשנייה מהמקור שעל הקרקע כפי שהאיש בראש המגדל סופר עבור האור מהמקור העליון. הוא יסיק מכך שבזמן ששנייה אחת עוברת אצלו פחות משנייה עוברת על הקרקע ומכאן שהזמן על הקרקע עובר לאט יותר מאשר בראש המגדל. תופעה זו נקראת התרחבות זמן כבידתית. שלא כמו בהתרחבות זמן כתוצאה ממהירות יחסית בין מערכות ייחוס כאן שני הצופים מסכימים על התשובה לשאלה איזה שעון מתקדם לאט יותר. הכלל הוא ששעון שנמצא במורד שדה הכבידה יתקדם לאט יותר ולא כפי שנאמר לפעמים בטעות, ששעון נע לאט יותר במקום שבו הכבידה חזקה יותר. נכון שבמציאות להיות במורד שדה הכבידה פירושו להיות קרוב יותר אל הגוף שיוצר את הכבידה ולכן גם הכבידה שם חזקה יותר, אבל התרחבות זמן כבידתית נכונה תיאורטית גם עבור שדה כבידה אחיד. התרחבות הזמן הכבידתית יכולה לעורר כמה תהיות. בתורת היחסות הפרטית יכולנו להציב שני צופים שנמצאים במערכות ייחוס שונות באותה נקודה בקירוב ובכך להימנע מהשפעות של המרחק והפרשי הזמן ביניהם. כשמדברים על התרחבות זמן כבידתית תמיד יהיו שני הצופים מרוחקים זה מזה ותמיד ייקח זמן להעביר אינפורמציה ביניהם. נושא האינפורמציה (אור למשל) מושפע מהכבידה בזמן המעבר בין הצופים. השאלה היא לכן: האם השעון במורד שדה הכבידה באמת מתקדם לאט יותר או שהוא רק נראה כך לצופה המרוחק? גם כאן השאלה איננה פיזיקאלית. הפיזיקה עוסקת בכללים ובמשוואות שמתארים את התנהגות הדברים בטבע. אין ספק בכך שהצופה המרוחק אכן מודד התרחבות של הזמן ביחס לצופה שבמורד שדה הכבידה ותורת היחסות הכללית יכולה לחשב ולצפות אותה. אין דרך להשוואת הזמנים של שני הצופים שאיננה תלויה במרחק ובזמן העברת האינפורמציה. השאלה אם ישנה איזו אמת אובייקטיבית שאיננה תלויה ביכולת שלנו לבדוק אותה נשארת שאלה פילוסופית.
עקרון האקוויוולנטיות נכון לחלוטין רק בשדה כבידה אחיד, אבל שדה כבידה אחיד לא קיים במציאות. אם אדם שנמצא בחללית שנופלת נפילה חופשית משחרר שני כדורים המרוחקים אנכית אחד מהשני, הכדור התחתון נתון לכבידה חזקה במקצת מזו של הכדור העליון ותאוצתו גדולה יותר. משום כך, עם הזמן המרחק בין הכדורים יגדל. לעומת זאת אם הוא ישחרר שני כדורים המרוחקים אנכית תהיה זווית קלה בין כיווני התאוצה של שני הכדורים מכיוון ששניהם מאיצים לכוון מרכז המסה של הכוכב אליו הם נופלים. שני הכדורים יתקרבו אחד אל השני עם הזמן. אם ענן של חלקיקים קטנים נמצא בנפילה חופשית לעבר גוף כבד, הוא משנה את צורתו עם הזמן: הוא נמתח בכיוון הנפילה ומתכווץ בכיוונים הניצבים לכוון הנפילה. אם גוף קשיח נופל נפילה חופשית יפעלו עליו כוחות מתיחה בכיוון הנפילה וכוחות מעיכה בניצב לנפילה. כוחות אלה נקראים כוחות גאות. כמובן שבחללית המשייטת במהירות קבועה בחלל הבין-כוכבי לא יהיו שום כוחות גאות וענן של חלקיקים ישמור על צורתו המקורית. לכן, אפשר להתייחס לעקרון האקוויוולנטיות כנכון בשדה כבידה בלתי אחיד רק באזור מצומצם שבו הכבידה היא לכאורה אחידה וכוחות הגאות הנם זניחים. העיקרון יהיה נכון לחלוטין רק עבור נקודה. לכן נאמר שעקרון האקוויוולנטיות הוא נכון רק מקומית.
הימצאותו של חומר גורמת לעיקום החלל-זמן בכל הכיוונים. החלל עצמו גם הוא עקום, כך ששני קווים ישרים (גיאודזיים) שהנם מקבילים באזור מסוים יעשו מוטים אחד ביחס לשני ויתקרבו או יתרחקו זה מזה באזור מרוחק. אבל ההשפעה של עקמומיות החלל היא לרוב מזערית ולא משמעותית. ראשית משום שלרוב אנו עוסקים במהירויות קטנות בהרבה ממהירות האור. מהירות כדור הארץ למשל במסלולו סביב השמש היא כ-1/10,000 ממהירות האור. כלומר בזמן שכדור הארץ מתקדם קילומטר אחד בכוון x למשל, הוא מתקדם 10,000 ק"מ בכיוון ct. ברור שבמהירויות כאלה השפעת עקמומיות החלל-זמן על הזמן (התרחבות הזמן) הרבה יותר משמעותית מהשפעתה על החלל. במרחקים קטנים יחסית העקמומיות זניחה ואפשר להניח שהחלל שטוח. כמו כן אם מדברים על מרחקים גדולים מאוד בחלל מתרחקים מהגוף שיוצר את שדה הכבידה והעקמומיות בכלל נעשית בלתי משמעותית. כשמוציאים את עקמומיות החלל מתוך משוואות תורת היחסות הכללית הן מקבלות את התבנית של חוק הכבידה האוניברסאלי של ניוטון. כך שחוק הכבידה של ניוטון הנו קירוב לתורת היחסות הכללית כאשר מדובר במהירויות נמוכות ושדה כבידה חלש, כמו שהמכניקה הקלאסית היא קירוב לתורת היחסות הפרטית עבור מהירויות נמוכות. עקמומיות החלל נעשית משמעותית כשמדובר במהירויות גבוהות ובגופים כבדים בעלי צפיפות גבוהה. אז עקמומיות החלל נעשית משמעותית ומשוואות הכבידה הקלאסיות לא נותנות תוצאות נכונות עבור התנועה של גופים. דוגמה לתנאים כאלה היא גוף קטן הסובב במסלול קרוב לכוכב נויטרונים. מסלולו של גוף כזה אינו אליפטי אלא בעל צורה מורכבת.
ישנם כמה ניסויים ותצפיות שמאשרים את נכונותה של תורת היחסות הכללית:
הטיית האור על ידי כבידה אושרה בתצפיות שנעשו בזמן ליקוי חמה מלא. בעת ליקוי חמה מלא ניתן לראות כוכבים בסמוך מאוד לשפת השמש. מדידות שנערכו על כוכבים שנראו מסביב לשמש בזמן ליקוי החמה הראו שהמרחק בין הכוכבים נראה גדול יותר מאשר כרגיל. הסיבה לכך היא שהאור הבא מהכוכבים הוטה על ידי שדה הכבידה של השמש.
הסט כבידתי לאדום נראה בניתוח הספקטרום של אור שבא מכוכבים צפופים מאד כמו ננסים לבנים וכוכבי נויטרונים. גם ניסויים שנעשו בשליחת אלומת לייזר במעלה מגדל הראו היסט קל לאדום כמצופה.
התרחבות זמן כבידתית נמדדה בעזרת שעונים מדויקים במטוסים ובחלליות. מערכת ה-GPS חייבת לקחת בחשבון את התרחבות הזמן הכבידתית כדי לקבל תוצאות מדויקות.
המסלול האליפטי של כוכב הלכת מרקורי (כוכב חמה) סוטה באיטיות בכיוון ההקפה של כוכב הלכת. מידת הסטייה לא יכולה להיות מוסברת באמצעות כבידה ניוטונית אך היא מתאימה לנוסחאות של תורת היחסות הכללית. מכיוון שמרקורי הוא כוכב הלכת הקרוב ביותר לשמש הוא נמצא בשדה כבידה חזק יחסית וגם נע במהירות גבוהה משאר כוכבי הלכת במערכת השמש. משום כך ניתן להבחין בהשפעת עקמומיות החלל על מסלולו.
כדי לערוך חישובים במרחב עקום נדרש כלי מתמטי שיוכל לתאר חלל עקום. התחום שעוסק בכך במתמטיקה נקרא גיאומטריה דיפרנציאלית. תיאור מתמטי של המרחב העקום מאפשר לנו לחשב מרחקים מהירויות וקווים גיאודזיים. השלב הבא הוא למצוא איך הימצאות חומר ואנרגיה משפיעה על עקמומיות החלל. משוואת השדה של איינשטיין מגדירה את הקשר הזה.
|