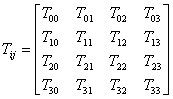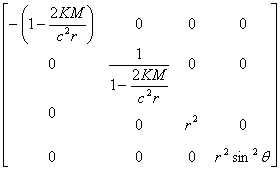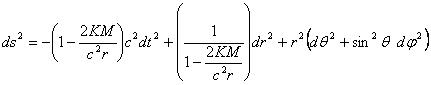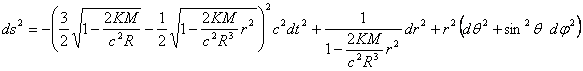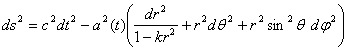עברית

אנגלית

דף הבית

משוואת השדה ועוד

טנסור איינשטיין

כפי שהוזכר בחלק הראשון של המאמר, משוואת השדה של איינשטיין היא משוואה שקושרת את הנוכחות של חומר ואנרגיה לעקמומיות החלל-זמן. בצד שמאל של המשוואה ישנו טנסור המייצג את עקמומיות החלל-זמן. זה אינו טנסור רימן המלא אלא טנסור שמייצג רק את עקמומיות ריצ'י. כדי שהמשוואה תראה פשוטה יותר זה גם לא טנסור ריצ'י עצמו אלא טנסור חדש שנקרא טנסור איינשטיין.  הטנסור הזה מחושב מתוך טנסור ריצ'י והמטריקה על פי הנוסחה הבאה:

כאשר G_ij הוא איבר של טנסור איינשטיין, R_ij הוא איבר של טנסור ריצ'י, R הוא סקלר ריצ'י ו- g_ij הוא איבר של המטריקה.

טנסור האנרגיה-מאמץ

בצד ימני של משוואת השדה ישנו טנסור אחר שמייצג את החומר והאנרגיה שנמצאים בנקודה. אנחנו זוכרים מתורת היחסות הפרטית שהם שקולים זה לזה. הטנסור הזה נקרא טנסור האנרגיה-מאמץ ומסמנים אותו באות T. טנסור האנרגיה-מאמץ מוגדר לרוב במונחים של 4-תנע. משום שהמשמעות של 4-ווקטורים איננה ברורה תמיד וביטויים כמו "שטף האנרגיה בכיוון הזמן" יכולים להיות מבלבלים, אנסה להשתמש במונחים מוכרים יותר. כמו טנסור ריצ'י גם טנסור האנרגיה-מאמץ הו טנסור מסדר (0,2) ומיוצג על-ידי מטריצה סימטרית לאלכסון בגודל 4x4:

ללא השורה העליונה והטור השמאלי נקבל מטריצה בגודל 3x3 שידועה כטנסור המאמצים. כל איבר במטריצה זו הנו המאמץ (כוח ליחידת שטח) בכיוון i שפועל על מישור ניצב ל-j . אם הכיוונים 1, 2 ו-3 הנם x, y ו-z בהתאמה, אז אם ניקח שטח זעיר במישור x,y, T₁₃ יהיה המאמץ שפועל עליו בכיוון x ו- T₃₃יהיה המאמץ שפועל עליו בכיוון z. האיברים באלכסון של המטריצה הם מאמצים נורמאליים כמו מאמצי מתיחה ולחיצה והאיברים האחרים הנם מאמצי גזירה. בתורת היחסות הכללית מדברים לעיתים קרובות על "נוזל אידיאלי". משמעות הדבר היא חומר שאין בו התנגדות לכוחות גזירה או מתיחה כמו גז או נוזל לא צמיג. בנוזל אידיאלי כל האיברים שמחוץ לאלכסון במטריצת המאמצים שווים לאפס והאיברים באלכסון הם חיוביים, זהים ושווים ללחץ בנקודה.

האיבר T₀₀ הוא צפיפות האנרגיה, כלומר האנרגיה לכל יחידת נפח בנקודה. האיברים T₀₁, T₀₂, T₀₃ הנם צפיפות התנע בכיוון j . T₀₁ למשל הוא התנע בכיוון x לכל יחידת נפח. האיברים T₁₀, T₂₀, T₃₀ אומרים לנו כמה אנרגיה עוברת דרך מישור ניצב ל- i ליחידת שטח ליחידת זמן. כאשר האנרגיה היחידה היא חומר במנוחה כל האיברים בשורה העליונה ובטור השמאלי, למעט T₀₀ שווים לאפס.

המשוואה

כעת יש בידנו כל הטנסורים הדרושים ואפשר לכתוב את משוואת השדה:

                                                                          (1)

כאשר K קבוע הכבידה של ניוטון.

המשוואה קושרת כל איבר של טנסור איינשטיין לאיבר המתאים של טנסור האנרגיה-מאמץ. מכיוון ששתי המטריצון הנן סימטריות לאלכסון מסתתרות במשוואה הטנסורית 10 משוואות שונות. עד כה דיברנו תמיד על טנסור בנקודה מסויימת. אבל ייתכן ונרצה לדעת את הקשרים האלה עבור כל הנקודות (אירועים) בתחום כלשהו של החלל-זמן. לשם כך נצטרך לדעת את ערכו של כל איבר של הטנסורים כפונקציה של המקום (שדה טנסורי). מכיוון שהחלל-זמן שלנו עקום יהיו אלה משוואות דיפרנציאליות חלקיות ואנחנו נשארים עם 10 משוואות דיפרנציאליות חלקיות.

טנסור האנרגיה-מאמץ בצידה ימני של המשוואה מכיל את כל האינפורמציה על פיזור החומר והאנרגיה בחלל-זמן, אבל טנסור איינשטיין בצידה השמאלי כולל רק אינפורמציה לגבי על עקמומיות ריצ'י שהינה רק חלק מהתמונה. משוואת השדה אומרת לנו רק איך העקמומיות בכל נקודה מושפעת מהחומר והאנרגיה שנמצאים באותה נקודה. אלה משפיעים רק על עקמומיות ריצ'י. עקמומיות ווייל בנקודה מושפעת על-ידי חומר ואנרגיה שנמצאים בנקודות אחרות. משוואת השדה אינה אומרת לנו דבר על עקמומיות וייל. כדי לחשב את עקמומיות וייל נזדקק למשוואות אחרות שקשורות לגיאומטריה של החלל-זמן בלבד ולידע על העקמומיות סביב הנקודות המרוחקות שגורמות להעקמומיות הזאת. בחלל ריק למשל אין חומר או אנרגיה (שדה כבידה אינו נחשב כאן לאנרגיה). העקמומיות (כבידה) היחידה בחלל ריק נגרמת על-ידי גופים מרוחקים. הדבר היחיד שמשוואת איינשטיין יכולה לומר לנו על חלל ריק הוא שעקמומיות ריצ'י שם שווה לאפס.

פתרון המסה הנקודתית

פתרון מדויק למשוואת איינשטיין הוא נוסחה עבור המטריקה בכל הנקודות (אירועים) בחלל-זמן, שמקיימת את משוואת השדה עבור מצב פיזיקלי ידוע. הפתרון המדוייק הראשון למשוואה היה הפתרון עבור מסה נקודתית שמצא קארל שוורצשילד זמן קצר אחרי פרסום תורת היחסות הכללית. הוא פותר את המקרה ההיפותטי של מסה שמרוכזת בנקודה אחת בתוך חלל ריק. הפתרון מתבסס על העובדות הבאות:

יש במקרה הזה סימטריה כדורית בחלל.

המקרה הוא סטטי. שום דבר לא משתנה עם הזמן.

טנסור איינשטיין כולו אפסים בכל נקודה למעט הנקודה שבה נמצאת המסה.

בגלל הסימטריה הכדורית יהיה זה רעיון טוב לבחור במערכת קואורדינאטות כדורית עבור החלל כך שקואורדינאטות החלל-זמן שלנו (0, 1, 2, 3) יהיו (t, r, θ, φ) כאשר t הוא הזמן, r הוא רדיוס של משטח כדורי סביב המסה הנקודתית ו- θ, ו- φ הם שתי זוויות בדומה לזווית האורך וזווית הרוחב בכדור הארץ. שימו לב שבשל העקמומיות של החלל, הרדיוס r אינו שווה למרחק מהמסה לנקודה שנמצאת על משטח כדורי באותו רדיוס, כפי שהרדיוס של קו רוחב אינו שווה למרחק מהקוטב אל נקודה שמצאת עליו. על-פי שלושת התנאים שלמעלה אפשר להראות שהשדה הטנסורי של המטריקה נתון על-ידי:

K הוא קבוע הכבידה של ניוטון, ו-M היא המסה.

אם נרצה לדעת את המרחק בין שתי אירועים סמוכים בחלל-זמן, נייצג אותו על-ידי ווקטור קטנטןds =  (cdt, dr, dθ, dφ) . נזין את הווקטור הזה פעמיים לטנסור המטריקה ונקבל:

                        (2)

משוואה מהסוג הזה נקראת משוואת אלמנט הקו.

מסתבר שהפתרון של מסה נקודתית נכון גם לגבי גוף כדורי במנוחה כמו כוכב שאינו סובב סביב צירו, עבור כל הנקודות שנמצאות מחוץ לכוכב.

הפתרון הפנימי

פתרון נוסף שמצא שוורצשילד הוא קירוב עבור המטריקה בתוך כוכב במנוחה.  שוורצשילד הניח שזהו גוף כדורי נייח שעשוי מנוזל אידיאלי בלתי דחיס. גם המקרה הזה הוא בעל סימטריה כדורית, אבל הפעם טנסור האנרגיה-מאמץ שלו אינו שווה לאפס. יש כאן צפיפות ולחץ בכל נקודה בתוך הכוכב. הצפיפות היא קבועה (זה המובן של בלתי-דחיס) והלחץ תלוי רק בקואורדינאטה r. משוואת אלמנט הקו של המטריקה הזאת היא:

                                                                                                                        (3)

עבור r ≤ R כאשר R הוא רדיוס הכוכב.

אפשר לראות שאם מציבים r = R ב-(2) וב-(3) מקבלים את אותה התוצאה, כך שיש רציפות בין הפתרון הפנימי לפתרון החיצוני.

חורים שחורים

הביטוי (2KM / c²) מופיע מספר פעמים גם במטריקה של הפתרון החיצוני וגם בזו של הפתרון הפנימי. הביטוי הזה הוא בעל יחידות אורך, הוא נקרא רדיוס שוורצשילד ומסומן על-ידי r_s. שוורצשילד הבחין שלפתרון המסה הנקודתית ישנה סינגולאריות כאשר r = r_s. אלמנט הקו ds נעשה אינסופי ברדיוס זה. שוורצשילד הניח שהסינגולאריות הזו איננה קיימת בטבע בשל העובדה שרדיוס הכוכב תמיד גדול מהרדיוס הזה. דבר זה נכון עבור כוכבים וכוכבי לכת רגילים. רדיוס שוורצשילד של השמש הוא שלושה ק"מ בעוד שרדיוס השמש הוא כ-700,000 ק"מ. רדיוס שוורצשילד של הארץ הוא כס"מ אחד בלבד.

מאוחר יותר הסתבר שהסינגולאריות אינה אלא סינגולאריות של הקואורדינאטות ולא סינגולאריות פיזיקאלית. סינגולאריות של קואורדינאטות היא מה שקורה למשל בקטבים של כדור הארץ. אין שום דבר גיאומטרי מיוחד בקטבים, אבל יש שם סינגולאריות כאשר אנו משתמשים במערכת הקואורדינאטות הכדורית של קווי האורך והרוחב.

מה בכל זאת קורה אם כוכב נעשה צפוף כל כך שהרדיוס שלו קטן מרדיוס שוורצשילד שלו? נסתכל קודם על הפתרון החיצוני. למרות שלא ניתן להשתמש במשוואה עבור רדיוס שוורצשילד עצמו, ניתן להשתמש בה עבור רדיוס קטן ממנו. המשוואה מראה דברים מוזרים בקשר לחלל-זמן שבתוך המעטפת הכדורית בעלת רדיוס שווה לרדיוס שוורצשילד. כל קו גיאודזי בתוך המעטפת הזאת שפונה למעלה אל המעטפת הוא קו דמוי חלל. אנו יודעים מתורת היחסות הפרטית שדבר לא יכול לנוע לאורך קו דמוי חלל, אפילו לא אינפורמציה. פירוש הדבר ששום חומר, אור או אינפורמציה לא יכולים לצאת מתוך המעטפת הזאת. יתר על כן, שום מסלול סביב הכוכב לא ייתכן בתוך המעטפת. כל דבר שנמצא בתוכה נופל כלפי הכוכב.

עוד יותר מוזר הוא מה שמתברר מתוך הפתרון הפנימי. בכוכבים רגילים יש איזון בין הכבידה ללחץ. הכוכב מגיע למצב של שיווי משקל שבו בכל נקודה הלחץ דוחף את החומר החוצה בדיוק במידה הדרושה כדי להתנגד לכבידה. בכוכב בעל רדיוס קטן מרדיוס שוורצשילד, שיווי משקל כזה איננו אפשרי. כפי שראינו קודם, הלחץ הוא חלק מטנסור האנרגיה-מאמץ והוא תורם לכבידה. ללחץ, אם כן, יש שתי השפעות מנוגדות: הוא דוחף את החומר החוצה ויוצר כבידה שמושכת את החומר פנימה. מסתבר שבכוכבים דחוסים כל כך לא משנה מה יהיה הלחץ, הוא אף פעם לא יספיק כדי לאזן את הכבידה. כתוצאה מכך הכוכב יקרוס פנימה עד אשר כל המסה שלו תהיה מרוכזת בנקודה אחת יחידה. בנקודה זו תהיה סינגולאריות פיזיקאלית.

התופעה הזאת נקראת חור שחור. התיאוריה צופה שכוכבים שנשארים כבדים פי שלושה ויותר מהשמש בסוף חייהם יהפכו לחורים שחורים. יש גם תצפיות שמעידות על קיומם של חורים שחורים ביקום. עבור חורים שחורים רדיוס שוורצשילד נקרא גם "אופק האירועים". באופק האירועים התרחבות הזמן הכבידתית הופכת אין סופית עבור צופה מרוחק והזמן שם לגביו עומד מלכת. כמו כן שום דבר שבתוך אופק האירועים איננו נראה לצופה מחוץ לו.

מודל היקום

אפשר להשתמש בתורת היחסות הכללית גם כדי ליצור מודל של כל היקום. בקנה מידה גדול מאוד אפשר להתעלם מהבדלים מקומיים בצפיפות החומר בחלל כמו גלאקסיות או מערכות שמש, ולהתייחס לחומר ביקום כאל נוזל אידיאלי. אנחנו עושים את אותו הדבר כאשר אנחנו מתייחסים למים כאל חומר אחיד ומתעלמים מהיותם מורכבים ממולקולות וחלקיקים אטומיים. מודלים של היקום מבוססים על שתי הנחות:

• היקום הוא הומוגני – כל הדברים זהים בכל נקודה ביקום.

• היקום הוא איזוטרופי – כל הדברים נראים אותו הדבר בכל הכיוונים בכל נקודה ביקום.

ההנחות האלה נראות נכונות עבור היקום הנראה לעיין, אבל אין לנו כל דרך לדעת אם הן באמת נכונות עבור כל היקום. צפיפות החומר ביקום יכולה להשתנות עם הזמן. היקום יכול להתפשט או להתכווץ. ההומוגניות והאיזוטרופיות מבטיחים סימטריה כדורית בכל נקודה ביקום כך שאנחנו יכולים לבחור כל נקודה כראשית ולהשתמש בקואורדינאטות הכדוריות המוכרות. המטריקה של יקום כזה נקראת מטריקת פרידמן-למיטרה-רוברטסון-ווקר (FLRW) ואלמנט הקו שלה נראה כך:

                     (4)

ישנם שני משתנים לא מוכרים במשוואה הזאת:

a(t) נקרא פקטור הסקאלה והוא מייצג את התפשטות היקום כפונקציה של הזמן.

k משמש לאיחוד של שלושה סוגי גיאומטריה אפשריים במשוואה אחת. הוא יכול לקבל אחד משלושה ערכים:

k = 0 – יקום שטוח

היקום בכללותו הוא אויקלידי והעקמומיות שלו שווה לאפס.

k = 1 – עקמומיות חיובית

העקמומיות בכל נקודה ביקום היא חיובית, כלומר, קווים גיאודזיים מקבילים יתכנסו במרחק. שלא כמו ביתר שני הסוגים של העקמומיות שיוצרים יקום אינסופי (פתוח), גיאומטריה כזאת יוצרת יקום סגור. יש לו נפח סופי והקווים הגיאודזיים שלו יוצרים מעגלים ענקיים. יקום כזה אנלוגי למשטח דו מימדי כדורי.

k = -1 – עקמומיות שלילית

העקמומיות בכל נקודה שלילית. קווים גיאודזיים מקבילים מתבדרים במרחק. אין אנלוגיה דו מימדית למרחב בעל עקמומיות שלילית שווה בכל נקודה. היפרבולואיד הוא בעל עקמומיות שלילית בכל נקודה אבל הוא אינו הומוגני והעקמומיות שונה בנקודות שונות.

סוג הגיאומטריה של היקום נקבע על-ידי היחס בין קצב ההתפשטות והצפיפות. עבור קצב התפשטות נתון יש צפיפות קריטית שעבורה היקום הוא שטוח. צפיפות נמוכה יותר תגרום לעקמומיות שלילית וצפיפות גדולה יותר תגרום לעקמומיות חיובית וליקום סגור.

סוג הגיאומטריה של היקום יקבע גם את עתידו. יקום פתוח ימשיך להתפשט לנצח. יקום סגור יעצור את התפשטותו בזמן כלשהו ויתחיל להתכווץ מחדש. עד כה התצפיות שנערכו לא נתנו תשובה חד משמעית לגבי סוג הגיאומטריה של היקום. ידוע שהוא שטוח בקירוב אבל ייתכן שיש לו עקמומיות חיובית או שלילית קלה.

כשאיינשטיין השתמש לראשונה בתורתו לצורך יצירת מודל של היקום הוא הניח שהיקום הוא סטטי. כדי שמשוואות תורת היחסות הכללית יתאימו ליקום סטטי היה צורך להוסיף למשוואות גורם נוסף שנקרא הקבוע הקוסמולוגי. ללא הקבוע הזה היקום היה צריך להתחיל להתכווץ כתוצאה מהכבידה שלו עצמו. מאוחר יותר,כשהאבל גילה שהיקום מתפשט, דבר שהוליד את תיאורית המפץ הגדול, הקבוע הקוסמולוגי לא היה דרוש עוד. מקובל היה לחשוב שהחומר שביקום נזרק לכל הכיוונים במפץ הגדול ומאז הוא מתפשט וקצב התפשטות יורד כל הזמן.

ממש לפני סיום המילניום הראו תצפיות שלמעשה היקום מאיץ את התפשטותו ולא מאט אותה. הקבוע הקוסמולוגי נשלף מקברו כדי לאפשר פתרון עבור יקום מאיץ. מתייחסים אליו היום גם כאנרגיית הריק או אנרגיה אפלה.