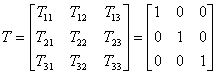Curved Space Geometry

Imagine a germ living inside the thin membrane of a soap bubble. We can see that the soap bubble is spherical and not flat because it is included in our flat 3D space in which it can be measured. As far as the germ knows he lives in a 2D space. At any point he can go in one of 2 perpendicular directions. For him the directions into the bubble and out of the bubble do not exist. But the germ can still notice that his 2D space is not flat. Two parallel "strait" lines (geodesics) get angled at a distance and also the sum of the angles in a triangle is more then 180º. This is because the bubble is internally curved. If his world had a shape of a cylinder he would not be able to tell that it is curved. Apart from the fact that in most directions, going a very long way strait ahead will surprisingly bring him to a known point, he would not see anything in the geometry of his world that is different from the geometry of a flat 2D space. A cylinder is only externally curved.

When we come to explore our 3D space or 4D space-time we are much like this germ. We can only look at it and measure it from inside. We cannot assume the existence of any higher dimension space in which it is embedded. And of course we can only talk about the internal curvature of it.

Tangent Vectors and Tangent Spaces

We know that a vector is an entity that has size and direction. But talking about directions in a curved space is somewhat tricky. If our germ in the bubble points ahead, we, the 3D creatures, can see that he is actually pointing in a direction that goes outside of his world. By pointing to some direction he draws a line that is tangent to the curved surface at the point where he is standing. If he goes strait ahead some distance and then points ahead again, we can see that he points to a different direction. Of course the germ can't see all that, but since he knows that his space is curved he can conclude that this is the picture. To every point on a curved surface there is a tangent flat surface (a plane). All the possible directions of the curved surface at this point can be defined within this tangent plane. In the same way, at every point on a 3D space or 4D space-time there is a tangent flat space in which we can draw all the possible directions of our curved space at this point. This is why we usually talk about tangent vectors and not just vectors in curved space geometry.

How do we calculate a length of a curved line? We know how to calculate the length of a strait line. So, we can approximately find the length of a curved line by dividing it to many segments small enough to be considered strait and sum their lengths. Calculus mathematics which I am trying to avoid in this article can reduce the size of these segments to zero increasing the number of segments to infinity, and get an exact result for the length of the curved line. In Differential Geometry that deals with curved spaces we do something similar. We know the rules of geometry in a flat space. We take a patch of space around a point, small enough to be considered flat and make geometrical calculations for this patch using the tangent flat space at this point. If we want to know sizes that are applied on larger part of space we have to sum over many such small patches that cover all the area (Or use calculus to integrate over all the desired space).

Tensors

The main mathematical tool for General Relativity is tensor calculus. We will only discuss here a little bit of this wide mathematical field. We will define two types of tensors that are needed for our purpose:

A rank (0,n) tensor is a linear function that takes n vectors and returns a number.

A rank (1,n) tensor is a linear function that takes n vectors and returns a vector.

These definitions are a little different from the general definition of tensor of rank (n,m) but they are equivalent to it and simpler.

Vectors are not necessarily defined by coordinates, but this is a very comfortable way to represent them if we want to make calculations on then. Let's look at an example: The dot product of vectors is given by a rank (0,2) tensor. It takes 2 vectors and returns a number. The general tensor equation of this operation on the vectors U and V can be written as:

If we chose a coordinate system and represent U and V by their coordinates so that:

and

Or, as we use to write in tensor calculus:

and

(A superscript in tensor calculus is an index of a vector component. For power operation we enclose the component in parenthesis.)

When using coordinates we can represent the dot product tensor T as a matrix of n x n numbers where n is the number of dimensions of our space. The components of the matrix are used as coefficients for the terms in the equation of the function. We know that the dot product of 3D vectors is given by:

(1)

The value of x is independent of the coordinate system. We get the same size of x no matter what coordinate system we choose (the value of x depends on the units of course).

We can write the dot product equation as a tensor equation like that:

(2)

This means: Take all the combinations of i and j and sum over the components that are the product of the ij component of the matrix T, the i coordinate of the vector U and the j coordinate of the vector V. Since we work in a 3D space, i and j can get the values 1 to 3. In order to save some writing Einstein set a convention that is known as Einstein's summation convention which says: "Whenever an index appears exactly twice in a term, we sum over all the possible values of that index." Using this convention we can rewrite (2) simply as:

(2.1)

(2.1) forms a sum of 9 terms where in (1) we have only 3. These are the components in which i=j. Also the coefficient of them all is 1. So, the matrix T looks like this:

What is the difference between superscript and subscript indices? They are used for different kind of entities. As we have seen superscripts are used for vectors. Subscripts are used for gradients. A gradient is the amount of change of some property per length unit. For instance, at some point on Earth, how much the air pressure changes per meter in each direction. Tensor components can have both superscripts and subscripts. They have one subscript for each input vector, the rest, if there are any, are superscripts. Vectors and gradients behave differently under coordinate system transformation. For instance, if we choose smaller units for our coordinate system, vector components will be bigger and gradient components, which are measured per unit, will be smaller. Things that behave like vectors are called contravariants and things that behave like gradients are called covariants.

In time-space we have 4 dimensions. For coordinate systems in time-space we use indices 0 to 3 where index 0 is used for the time direction.

Parallel Transport

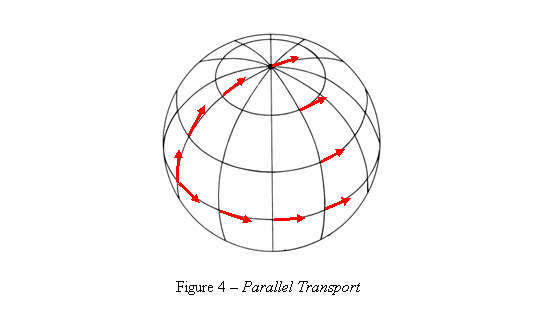
A parallel transport is an operation that takes a tangent vector and moves it along a path in space without turning it (relative to the space) or changing its length. In flat space we can say that the transported vector is parallel to the original vector at every point along the path. In curved space we cannot say such a thing. Let's use the spherical surface of Earth to show this: We start at the equator at longitude 0 holding an arrow pointing north (Fig. 4). We go along longitude 0 up to the North Pole, keeping our arrow parallel to the ground and pointing forward all the time. When we get to the North Pole our arrow is pointing in the direction of longitude 180°. Now we go south along longitude 90° east keeping our arrow perpendicular to our path as it was at the North Pole. When we get to the equator our arrow is pointing to the east. Finally, we go west along the equator until we get back to our starting point. We keep the arrow pointing backwards all the way. Though we did not turn the arrow all the way, we are now at the starting point with our arrow turned 90° relative to its original position. We surely can't say that it is now parallel to the original position. This means that the term "direction" cannot be defined globally in a curved space. We can only compare the direction of two vectors if they are at the same point.

The fact that parallel transport along a closed loop changes the direction of a vector in a curved space but not in a flat space may lead to the idea of using it as a way to measure curvature. We cannot prove it mathematically here, but it turns out that if we choose a loop that is small enough around a point in a curved space, the amount of change in the direction of a vector that is parallel transported along it is proportional to the area enclosed by the loop. So, the ratio between the area of the loop and the amount of change in the direction of the vector (whatever way we chose to measure it) can be used as a measure to the curvature of the surface that includes the loop. Actually we define curvature by the value of this ratio.

Riemann Curvature Tensor

Riemann tensor is a rank (1,3) tensor that describes the curvature in all directions at a given point in space. It takes 3 vectors and returns a single vector. The vectors that are fed to the tensor should be very small and have a length ε. If we use the first two vectors to form a tiny parallelogram and we parallel transport the third vector around this parallelogram, the vector that the function returns is approximately the vector difference between the original vector and the vector after the parallel transport. Mathematically it can be written like this:

Where U and V are the vectors of length ε that form the parallelogram, R is Riemann tensor, W is the third vector before the parallel transport and W' is the vector after the parallel transport. Note that ε³ get smaller much faster then ε² as we reduce the value of ε, so that for any required precision we can choose ε small enough so that the terms of ε³ will be negligible and we can write:

Using coordinates it will look like this:

R is now a 4-dimensional matrix with (N)⁴ components where N is the number of dimensions in our space. By summing over j,k and l we can find any component of the vector which is the difference between W and W'. This vector can be thought of as the vector that connects the ends of W and W'.

The Metric

The metric is a very important concept in curved space geometry. It lets us calculate sizes of vectors and angles between vectors. This is actually what we need to know about vectors. The metric is a tensor of rank (0,2). It takes two vectors and returns a number. In Euclid space the metric is defined as the dot products of two vectors as we have seen in the section about tensors above. If we feed this tensor with the same vector twice, the number we get is the square of the length of the vector. If we feed it with two different vectors, the number we get is the product of the lengths of the vectors times the cosine of the angle between them. Once we know the lengths of the vectors we can use the metric to find the angle between them.

In a flat time-space (also called Minkowsky space) the metric or the inner product of two vectors is defined similarly, just the sign of the time component is inverted. We have shown in "Understanding Special Relativity" that the metric for two dimensional time-space is:

In 4D time-space it will be:

Or if we write it as a tensor:

We sum over i and j that go from 0 to 3. The matrix g looks like this:

The matrix of the metric has this nice diagonal form only because of the way we have chosen the coordinate system, more specifically, because the coordinates are independent of one another (orthogonal). If we choose the coordinates arbitrarily, the diagonal elements might not be ones and the rest of the elements of the matrix will not be zeros. In a flat space or time-space we can chose such independent coordinates and use them for the whole space. In a curved space there is no global coordinate system. We can of course select such a set of coordinates within the tangent space of every point in the curved space, but this means that we change our coordinate system as we move from point to point. If we want to make calculation on a range in space or time-space we need a mathematical description of the way the coordinates are changed as we move from one point to the next point. Mathematics uses the notion of derivative to describe how something is changing in space. This is relatively easy when we have a global coordinate system like in the case of spherical surface that is included in a Euclid 3D space. It gets a little harder when we have to do it internally without a global coordinate system (remember the germ in the soap bubble). Mathematics introduces for this purpose a new concept called covariant derivative. With this tool in hand mathematicians can write an equation that relates the metric tensor components to the Riemann curvature tensor. This equation is pretty scary and full of frightening signs and we will not even start to get into it here. For those who are brave enough and want to see what it looks like, your keywords are "Christoffel symbols" and "metric connection".

Ricci Tensor, Weyl tensor and Ricci Scalar

Riemann Tensor has 256 components in 4D time-space. Fortunately there are some groups of components that are the same or the negative of others. Also there are some groups of components that their sum equals 0. Taking all this into account, there are only 20 independent components in Riemann tensor from which we can build the whole tensor.

Ricci tensor is a rank (0,2) tensor that can be calculated from Riemann tensor by the following formula:

To make things even less clear than they are, mathematicians sign Riemann tensor, Ricci tensor and Ricci scalar all with the letter R. We can distinguish between them only by the number of indices: 4 indices for Riemann tensor 2 for Ricci tensor and none for Ricci scalar. The formula above says that we calculate any component R_ik of Ricci tensor by summing all the components of Riemann tensor that their second index is i the forth index is k and the first and third indices are the same. Ricci tensor depends only on 10 of the 20 independent components of Riemann tensor. Ricci tensor itself is diagonally symmetric, so in 4D time-space it has 10 independent components out of its 16 components. We can say that Ricci tensor represent 10 of the independent components of Riemann tensor. The rest 10 independent components of Riemann tensor are represented by Weyl tensor. Weyl tensor has the same form as Riemann tensor but in addition to all the component dependencies in Riemann tensor all the components of its Ricci tensor are zeros. That is:

So, Weyl tensor is also a 256 components tensor but it has only 10 independent components.

Ricci scalar is a number that is calculated from Ricci tensor by this formula:

Where g^ij is called the metric inverse and can be calculated from the metric g_ij.

The Geometric Meaning of Curvature Tensors

A point (0D) cannot have any curvature. A line (1D) can only have external curvature: There is no loop along which we can parallel transport. The external curvature of a line can be characterized by the local radius at a point. 2D is the lowest dimension space that can have internal curvature. The example of spherical surface that we have used is a very simple case. It has the same radius in every direction at every point. For more general curved surface we have different radii in different directions at a point like in the case of an ellipsoid for example. But a radius is something that we can talk about from an external point of view. Internally we can only talk about the results of a parallel transport around a tiny parallelogram. In 2D the original and the returned vectors are both in the tangent plane at the point. The length of the vector does not change during parallel transport, so the returned vector can differ from the original only by the angle between them. It can be shown that this angle does not depend on what parallelogram we choose but only on the area of it. Thus, all the information about the internal curvature of a 2D surface at a given point can be described by a single number. In differential geometry Ricci scalar can tell us everything about the curvature of a 2D surface. All the 4 components of 2D Ricci tensor and the 16 components of 2D Riemann tensor can be calculated from this single scalar.

Another way to look at the internal curvature is to examine the geodesics deviation. We know that on curved surface geodesics that are parallel at some region get angled and change the distance between them as we advance along them. They get closer on a sphere or ellipsoid and farther apart on a hyperboloid (a saddle-like surface). Any point on a curved surface can be locally ellipsoid, locally flat or locally hyperboloid. Now, if we take a very short line at some point of the surface and start moving all its points along geodesics perpendicular to the line, the line will change its length. At the starting point the geodesics are parallel and thus the length of the line does not change but it already start changing the rate at which its length is changed (If I was using calculus terms – which I don't – I would say that the second derivative of the length of the line is nonzero). We can think about the following analogy: as we drop something, at the moment we let it go its velocity is 0 but it already have acceleration equals to g. This rate at which the small line starts changing its length is the geodesic deviation at this point. In curved 2D surface its value is the same in all directions.

With curved 3D space we need 6 numbers to completely describe the curvature at a point. Obviously Ricci scalar is not enough here. 3D Ricci tensor has 9 elements, but since it is diagonally symmetric, only 6 of them are independent. Ricci tensor can describe everything about 3D curvature and all the 81 elements of the Riemann tensor can be calculated from the Ricci tensor. What about geodesic deviation? We can do something similar to what we did in 2D: We take a little circle and examine how it starts changing as we move all its points along geodesics that are normal to the plane of the circle. Note that if the rate of the change is the same in all directions, it will preserve its circular shape and only change its size, but if the rate is not the same in all direction it will turn into an ellipse. The 6 independent components of Ricci tensor can describe these changes in any selected direction in the curved 3D space.

We have seen that in 4D space, Riemann tensor has 256 components from which 20 are independent. So, we need 20 numbers to completely describe the curvature of 4D space at a given point. To examine the geodesic deviation we take a small ball and move all its points along geodesic in the forth dimension. Again the ball can change its volume and can also change its shape to an ellipsoid. The 10 independent components of Ricci tensor describe how the volume of the ball starts changing in any given direction. Weyl tensor describes how it changes its shape. If Weyl tensor is all zeros but Ricci tensor is not, the ball will only change its volume but not its shape. If Ricci tensor is all zeros but Weyl tensor is not, the ball will be changed into an ellipsoid without changing its volume. In 4D (and up) we can talk about two independent types of curvature: Ricci curvature and Weyl curvature. The complete curvature of the space is a combination of these two types of curvature.

What can we learn from all this? We can see that the examples with a 2D curved surface we use are very limited. 2D surface has only scalar curvature and no Ricci or Weyl curvature. The real fun in curved space geometry starts at 4D where we can have both Ricci and Weyl curvature. Unfortunately, our brain is only capable of visualizing 3 dimensions. Since we need one dimension in which to curve our space, the most we can visualize is a curved 2D surface. Thus, we cannot really grasp the meaning of Ricci or Weyl curvature, just as we cannot really understand how in flat 4D space a plane can be used as an axis of rotation (it can). We can accept it, we can calculate it, but we cannot visualize it. This is why we usually use pure mathematics to describe curved space-time and almost give up trying to understand the meaning of it.