|
The Principles of General Relativity
Once when Einstein was preparing for a review of his (not yet called special) theory of relativity, he thought about the fact that a man falling from the roof of a building doesn't feel his own weight. This thought which he later described as "The happiest thought of my life", was the seed from which the theory of General Relativity grew. The idea of general relativity is not very hard to understand. The mathematics of it is quite complicated and involves curved space geometry that is not easy to comprehend. Einstein had struggled with the mathematics of his theory for several years before he got to the correct version of his famous field equation. Though looks quite simple, this equation actually includes 10 different differential equations, and cannot be used in practice as it is. Einstein did not expect exact solutions for his equation to come soon. Surprisingly the first solution for the equation was found by Karl Schwarzschild a few months after Einstein published his final version of the General theory of Relativity in 1915. This solution describes the gravity field around a massive static spherical body. No other solutions were found until the sixties when new mathematical tools where developed and computers became available.
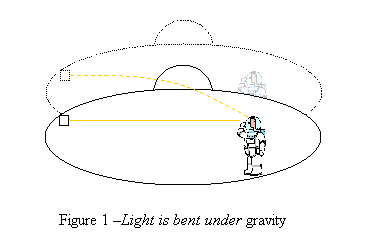
If a space-ship is in a free fall, everything in it seems weightless. A man inside a closed spaceship would not be able to tell whether his spaceship is freely falling or cruising at a constant speed in the interstellar space where no significant gravity exists. Any mechanical experiment he might do would give the same result in both cases. Also, the man in the closed spaceship would not be able to tell whether his spaceship is parking on the surface of a planet or accelerating at a constant acceleration in the interstellar space. Einstein suggested that this is not just a similarity in the behavior but actually the same physical states. In other words, a freely falling frame in a gravity field is equivalent to an inertial frame with the absence of gravity. Also, a static frame in a gravity field is equivalent to an accelerating frame with the absence of gravity. But wait! What about light? If this equivalence is true than in a gravity field, light pulse move in a straight line relative to a freely falling frame but relative to a static frame it is bent downwards (Fig. 1). Is light also affected by gravity? General Relativity predicts that it does, and this prediction has been confirmed by observations of star light and by experiments.
Einstein said that gravity can be looked at as curvature in space-time and not as a force that is acting between bodies. (Actually what Einstein said was that gravity was curvature in space-time and not a force, but the question what gravity really is, is a philosophic question, not a physical one and we will not get into it here.) How can we explain the behavior of objects in a gravity field by curvature of space-time? To understand this let us look at a curved system that is known to all of us - the surface of Earth. First we have to find an equivalent to a strait line on our curved surface. We can define such line as the shortest path between two points, or alternatively, a line that as we go along it we don't turn relative to the curved surface (we only turn with the curvature of the surface). Such line is called a geodesic. On a spherical surface it will be a great circle, that is, a circle that its center is at the center of the sphere. Longitudes, for instance, are geodesics.
Now, imagine two ships starting at two points on the equator and moving at the same velocity strait to the north. At first they sail parallel to each other. But after some time they start getting closer and closer in the east-west direction. If time-space is curved in such way that two geodesics in time direction get closer and closer in space, we will see two bodies that start at rest relative to each other (moving only in time) beginning to move towards each other just as if some force attracts them. What if we want to keep a constant distance between two bodies in a gravity field? Let's look again on the model of the Earth surface. The distance between two latitudes is constant. But latitudes, with the exception of the equator, are not geodesics. Going along a latitude means continuously turning relative to Earth's surface. If it is hard for you to see it, think about a latitude very close to one of the poles; say a circle with a radius of 10 meters around it. Obviously, if one wants to follow this circle he must continuously turn. So, if two sailing ships need to keep a constant distance between them, at least one of them must turn away from the other all the time. Similarly, in a gravity field a constant force is needed to keep one body at a constant distance from the other. We can now change a little the first law of Newton and instead of saying that without any force acting on them bodies are moving at a constant speed along straight lines, we say that without any force acting on them bodies are moving along geodesics in space-time. Where no gravity is present, time-space is flat (in this context flat means not curved), and these geodesics are straight lines in time-space or a constant speed along straight lines in space. With the presence of massive bodies, time-space is curved and geodesics can be a constant acceleration along straight lines in space (free-fall), an orbit around the center of mass of a heavy body, or any other known behavior of bodies in a gravity field. Gravity field is not a force field but curvature of time-space caused by the presence of mass and energy.
Gravitational Redshift and Time Dilation
Let's look at the following scenario: A very large spaceship is accelerating in the interstellar space in a direction we call upwards. On the floor of the spaceship there is a light source. While the light travels from the floor to the ceiling, the spaceship gains some velocity. When the light gets to the ceiling, the spaceship is moving away from the source of the light as it was when the light was transmitted. Because of the Doppler effect, an observer at the ceiling will see the light frequency shifted to red (lower frequency) compared to an observer near the light source. Similarly, an observer on the floor will see light coming from a source near the ceiling shifted to blue (higher frequency). The equivalence principle tells us that the same must be true for a stationary spaceship on the surface of a planet. So, a man on the top of a tower will see light coming from the ground red-shifted and a man on the ground will see light coming from the top of the tower blue-shifted. This phenomenon is called gravitational redshift. Now suppose there are two identical laser sources one on the ground and the other on the top of a high tower. An observer on the top of the tower has an instrument that counts the cycles of light waves. He activates the instrument for exactly one second, and compares the number of cycles of light from the source near him to the number of cycles of the light from the ground. Since the light from the ground is red-shifted, he counts more cycles of the upper source then these of the ground source. But he knows that the two light sources are identical and thus, an observer on the ground would count the same number of cycles per second as he counts for his light source. He concludes that while one second passes for him, les than a second pass on the ground, or that time pass slower on the ground. This is called gravitational time dilation. Unlike time dilation due to relative velocity, here the two observers agree on whose clock runs slower. The rule says that clocks lower in the gravity field runs slower and not, as sometimes mistakenly said, that clocks run slower where gravity is stronger. It is true that in nature, lower in the gravity field means closer to the attracting body and thus stronger gravity, but gravitational time dilation is also true for hypothetical uniform gravity field. Gravitational time dilation may raise some questions. In Special Relativity we could put two observers in different reference frames at nearly the same point, and by that eliminate effects of the distance and the time difference between them. With gravitational time dilation there is always a distance between the observers and it always takes time for information to get from one point to the other. The carrier of the information (light for instance) is affected by gravity during this time. The question is then: Does the lower clock really run slower or dose it only look so to the distant observer? Once again, this is not a physical question. Physics deals with rules and equations that describe the behavior of nature. There is no doubt about the fact that the distant observer does see time dilation, and General Relativity can calculate and predict it. There is no way to compare the time of the two observer which is independent of the distance and the limit on the speed at which information can be transferred. The question whether there is some objective truth that is independent of our ability to measure it remains a philosophic one.
The equivalence principle is absolutely true only in a uniform gravity field. But uniform gravity field does not exist in the real world. If a man in a freely falling spaceship releases two balls that are vertically distant from each other, the lower one is subject to a slightly stronger gravity then the upper and accelerates faster. So, as time progress the distance between the balls grows. On the other hand, if he releases two balls horizontally distant, there is a slight angle between the directions of their acceleration because they accelerate towards the center of mass of the planet. So, as time progress the distance between them gets smaller. If a cloud of small particles is freely falling towards a heavy body, it changes its shape with time. It stretches in the direction of the falling and shrinks in directions perpendicular to it. If a rigid body is freely falling it will be subject to forces that stretch it in the direction of the fall and press it in the directions perpendicular to it. These forces are called tidal forces. Of course, in a spaceship cruising in space without any gravity, there would be no tidal forces and a cloud of particles will retain its original shape. Thus, the equivalence principle in non uniform gravity field can be considered true only for a very small space in which the gravity field is practically uniform and tidal forces are negligible. It would be absolutely true only at a point. We say that the equivalent principle is only locally true.
The presence of matter curves space-time in all directions. Space itself is also curved so that two strait (geodesic) lines in space that are parallel at some area get angled and closer or farther apart at a distance. But the effect of the curvature of space is usually minor and negligible. First because we usually talk about velocities that are much lower then light speed. For instance the speed of the Earth in its orbit around the Sun is about 1/10000 the speed of light. That is, while Earth moves one kilometer in say x direction it moves 10,000Km in the ct direction. Obviously the effect of the curvature on time (time dilation) is much more significant than this of the curvature in space directions. In small distances curvature is negligible and space can be considered flat. In addition when we talk about very long distances in space we may get far away from the body that cause the gravity field, and curvature in all directions of space-time gets very small. When we eliminate space curvature from the equation of General Relativity, it gets the form of Newton's law of universal gravitation. So Newton's low of gravitation is an approximation to General Relativity for low speeds and week gravity field, just as classic mechanics is an approximation to Special Relativity for low speeds. Space curvature gets significant when we deal with high speeds and very dense and massive bodies. Then, space curvature gets significant and classic gravitation equations do not predict the motion of bodies correctly. An example for such conditions is a small body in a close orbit around a neutron star. Its orbit is no longer elliptic and has a complex shape.
Verifications of the GR Theory
There are some known experiments and observations that verify the theory of General Relativity:
The bending of light by gravity has been shown by observations made during a total solar eclipse. At a total solar eclipse stars can be seen very close to the limb of the Sun. Measurements done on stars that appeared around the Sun during the eclipse showed that the distance between the stars looked greater then usual. The reason for this was that the light coming from the stars was bent by the gravity of the Sun.
Gravitational redshift has been shown by examining the spectrum of light coming from heavy starts like white dwarfs and neutron starts. Also experiments done on Earth by sending laser beams up a high tower could show the slight expected redshift.
Gravitational time dilation could be measured using precise clocks on planes and satellites. The Global Positioning System must take the gravitational time dilation into account to get accurate results.
The elliptic orbit of the planet Mercury is turning slowly in the direction of the orbit. The amount of this change in the orbit could not be explained by Newtonian gravity but it matches the equations of GR. Since Mercury is the closest planet to the Sun it is in a relatively strong gravity field and it also moves faster the other planets in the solar system. The effect of space curvature on its orbit is noticeable.
To make physical calculations in curved space we first need mathematical tools to describe a curved space. The field in mathematics that deals with it is called Differential Geometry. Once we have a mathematical description of the curved time-space we can calculate distances velocities and geodesics. The next step is to find out how the presence of matter and energy curve time-space around them. This is what Einstein's field equation does.
|