התנגשות אלסטית יחסותית במימד אחד

 

 

בהתנגשות אלסטית התנע הכולל והאנרגיה הכוללת נשמרים ולכן:

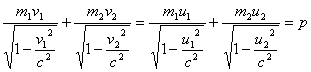                                          (1)

 

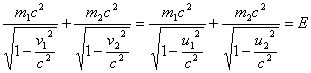                                          (2)

 

 

 

כאשר m₁ ו- m₂הם המסות של הגופים המתנגשים, v₁ ו- v₁הם מהירויות של הגופים לפני ההתנגשות ו- u₁ו- u₂הם המהירויות אחרי ההתנגשות.

אם ננסה לפתור את המשוואות האלה ולמצוא את u₁ ו- u₂נקבל משוואות מסדר גבוה שלא ניתן לפתור אותן באלגברה. נזדקק לכמה יחסים פיזיקלים ידועים כדי להגיע למשוואות פשוטות יותר.

 

ראשית, אפשר להראות בעזרת הצבה שבמקרה הפרטי שבו התנע הכולל שווה לאפס הערכים  ו- נותנים פתרון נכון לשתי המשוואות (גם  ו- נותנים פתרון נכון אלא שבמקרה זה אין כל התנגשות).

אפשר, לפיכך, למצוא מערכת ייחוס שבה התנע הכולל של המערכת שבה אנו עוסקים הוא אפס, למצוא את המהירויות של הגופים לפני ההתנגשות במערכת ייחוס זו, למצוא את המהירויות אחרי ההתנגשות במערכת ייחוס זו פשוט על ידי הפיכת סימנן ואז להמיר את המהירויות החדשות למערכת הייחוס המקורית.

מהירויות ממירים בין מערכת ייחוס אחת לשניה על ידי נוסחת צירוף המהירויות: 

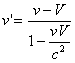                                                                                                     (3)

 

 

 

כאשר v הוא המהירות במערכת הייחוס המקורית, V הוא מהירות מערכת הייחוס החדשה בייחס למערכת הייחוס המקורית, ו-v' הוא המהירות במערכת הייחוס החדשה.

אבל איך נוכל מצוא את המהירות V של מערכת הייחוס שבה התנע הכולל שווה לאפס?

 

הנה שתי שיטות להגיע לאותה משוואה עבור V:

 

גירסת המתמטיקאי*:

 

טרנספורמציית לורנץ עבור תנע הנה:

 

כך שאם  S' היא מערכת הייחוס שבה התנע הכולל שווה לאפס יהיה:

 

 

כאשר   γ_Vאינו אפס יהיה:

 

                                                                                                         (4)

 

 

 

* מתמטיקאי אמיתי היה למעשה פותר את המקרה הכללי של n גופים שנעים בשלושה מימדים בעזרת טרנספורמציה של 4-ווקטור ואז היה מציב n=2 ו- v_i=0 עבור כל כוון מלבד x; אבל כאן מדובר כנראה במתמטיקאי עצלן.

 

גירסת הפיזיקאי:

 

אנו יודעים כי . ניתן כנראה לפתור את המשוואה עבור V אך לשם מה לנו לטרוח? אפשר לראות ש-V פונקציה של E ו-p ומכאן שלכל מערכת שלה  p ו-E זהים תהיה גם המהירות של מרכז המסה V זהה. אנו יודעים שעבור גוף בודד מתקיים:

ולכן נוסחה זו תקפה עבור כל מערכת.

 

לאחר שמצאנו את המהירות V אפשר למצוא את המהירויות לפני ההתנגשות במערכת הייחוס של מרכז הכובד (שבה התנע הכולל שווה לאפס) על ידי:

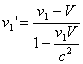                                                                                                   (5)

 

 

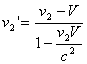
                                                                                                                         (6)

 

לאחר מכן משנים את הסימן של המהירויות וממירים אותן חזרה למערכת המקורית כדי למצוא את המהירויות אחרי ההתנגשות:

 

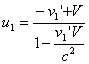                                                                                                  (7)

 

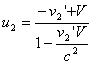                                                                                                 (8)