Relativistic One Dimensional Elastic Collision

 

 

In an elastic collision the total energy and the total momentum are preserved:

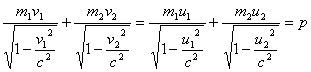                                            (1)

 

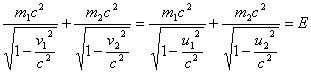                                          (2)

 

 

 

Here, m₁ and m₂ are the masses of the colliding bodies, v₁ and v₂ are the velocities of the bodies before the collision and u₁ and u₂ are the velocities after the collision.

If we try to solve this set of equations for u₁ and u₂ we get equations of high power which cannot be solved by algebra. So we use some known relations of physics to get simpler equations.

 

Firs, we can show by substitution that in the special case when the total momentum equals zero,  and  is a correct solution to the equations (So is  and but then there is no collision).

So, we can find a reference frame in which the total momentum for the system in question equals zero; find the velocities before the collision in this frame, find the velocities after the collision in this frame just by changing their signs, and then transform the new velocities to the original frame.

We transform velocities between frames with the velocity composition equation:

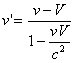                                                                                                      (3)

 

 

Where v is the velocity in the original frame, V is the velocity of the new frame relative to the original frame and v' is the velocity in the new frame.

But how can we find the velocity V of the frame in which the total momentum is zero?

 

Here are two ways to get the same equation for V:

 

The mathematician's way*:

 

Lorentz transformation for the momentum is:

 

 

So if S' is the reference frame in which the total momentum is zero, we have:

 

 

When γ_V is not zero we have:

                                                                                                         (4)

 

* Actually a real mathematician would have solved the general case of n bodies moving in 3 dimensions using 4-vector transformation and then substitute n=2 and v_i=0 for every direction other than x; but this one is a lazy mathematician.

 

The physicist's way:

 

We know that . We cam probably solve it for V, but why bother? We can see that V is a function of E and p, so every system with the same p and E has also the same center of mass velocity V. We know that for a single body we have:

 

 

 

So this must be true for any system.

 

Once we have found V we can get the velocities before the collision in the frame of the center of mass (where the total momentum equals zero) with:

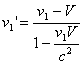                                                                                                   (5)

 

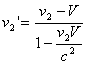                                                                                                  (6)

 

 

Then change their sign and transform them back to the original frame to find the velocities after the collision:

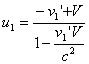                                                                                                  (7)

 

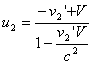                                                                                                 (8)